Наклон по вертикали
Измерение отклонений конструкций от вертикали
Обмерные работы
Приборы
ИНСТРУМЕНТАЛЬНЫЕ ИЗМЕРЕНИЯ
2.1. Для измерений геометрических размеров и величин деформаций и перемещений конструкций (наклонов, выпучивания, перекосов, сдвигов) используются следующие измерительные приборы:
приборы для линейных измерений в плане, по ширине (толщине) и высоте конструкций
— стальные и деревянные линейки, складные метры;
— стальные и тесмянные ленты и рулетки длиной 5, 10, 20 м и более;
приборы для угловых измерений
— обыкновенные и прецизионные теодолиты с 20-40-кратным увеличением трубы и минимальным расстоянием визирования 1,5-2 м (ТБ-1, ТТ-5, ОТШ, ТОМ, ОТ-2 и др.);
приборы для определения вертикальных перемещений
— обыкновенные и прецизионные оптические нивелиры с 20-30-кратным увеличением трубы и минимальным расстоянием визирования 1,3-2 м (НЗ, НВ-1, НТ, НА-1);
— оптические теодолиты с накладным уровнем на трубе (ТТ-4; ТОМ; ОТШ);
— гидростатические нивелиры (уровни), основанные на принципе сообщающихся сосудов типа НШТ и др., применяются для нивелирования в тесных, захламленных и сложных в плане помещениях, подвалах, коммуникационных траншеях и т.п.; точность отсчетов невооруженным глазом — 0,5 мм, при использовании специальных поплавков — до 0,1 мм;
приборы для проверки вертикальности конструкций, зданий и сооружений
— проволочные и нитяные отвесы длиной до 20 м и весом до 5 кг;
— оптические приборы вертикального визирования с 30-кратным увеличением трубы (зенит- и надирприборы ОЦП, ПОВП);
— лазерные приборы (ПМЛ-1, ЛЗЦ-1, лазерный теодолит ЛТ-75).
2.2. Обмеры зданий и конструкции по длине, ширине и высоте выполняются с помощью стальных лент, рулеток, линеек, угольников, отвесов, штангенциркулей и т.п. Точность измерений сечения и длины бетонных и каменных конструкций — 1 см, стальных элементов и арматуры — 1 мм. Результаты измерений наносятся на заранее заготовленные планы, разрезы, схемы узлов и сечений конструкций. Размеры и положение конструкций и их узлов в плане и по высоте должны увязываться с общими размерами зданий и результатами геодезической съемки (вертикальной и горизонтальной).
2.3. Отклонение от вертикали и выпучивание конструкций зданий и сооружений большой высоты (трубы, башни и т.п.), а также в труднодоступных местах, определяются с помощью теодолитов методом сноса вертикали (проектирования) на линейку с миллиметровыми делениями (рис. 1).
2.4. Отклонение от вертикали в пределах этажа стен, перегородок, столбов и колонн (наклоны, выпучивание, смещение по горизонтали и т.п.) определяются с помощью нитяных и проволочных отвесов диаметром от 0,2 мм до 1-2 мм, закрепленных на кронштейнах, стойках или вышележащих конструкциях. При использовании отвесов отклонения от вертикали стен, столбов и перегородок в характерных точках (рис. 2, а) находятся как разность расстояний рассматриваемых точек ai до отвеса относительно низа рассматриваемого элемента (нулевой точки). Измерение удаления точек от отвеса выполняется с помощью линейки с миллиметровыми делениями при строго горизонтальном ее положении; точность измерений при отсчете на глаз ±0,5 мм.
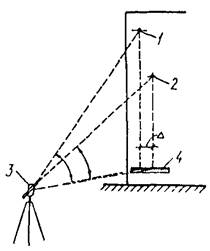
Рис. 1. Измерение горизонтального смешения, двух точек (1 и 2) стены здания методом сноса вертикали с помощью теодолита
1, 2 — точки; 3 — теодолит; 4 — переносная линейка с миллиметровыми делениями
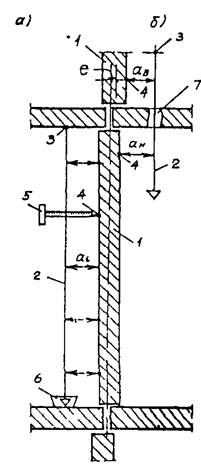
Рис. 2. Определение соосности (б) и отклонений стен от вертикали (а) с помощью вертикального отвеса
1 — стеновые панели (перегородки); 2 — отвес; 3 — точки подвески отвеса; 4 — точки измерения; 5 — линейка; 6 — сосуд с водой; 7 — отверстие в перекрытии
2.5. Соосность стен (панелей) различных этажей и величина горизонтального смещения осей стен в уровне перекрытий определяются с помощью отвесов, пропущенных через швы или отверстия в перекрытиях (рис. 2, б).Величина горизонтального смещения (эксцентриситет) осей стен (панелей) вышележащего и нижележащего этажей находится как разность расстояний от их поверхностей до отвеса (с учетом толщины стен).
Источник: https://studopedia.ru/1_2444_izmerenie-otkloneniy-konstruktsiy-ot-vertikali.html
Трансформация
Сама матрица преобразований предназначена для вычисления новых координат элемента с целью его трансформации. При этом соблюдается условие, что линии всегда остаются параллельными, поэтому в качестве трансформации допустимы поворот, масштабирование, наклон и изменение положения, но никак не перспектива или нечто подобное. На рис. 1 показаны допустимые и невозможные преобразования, сделанные с помощью матриц.
 |
 |
 |
 |
| Исходный элемент | Поворот | Наклон | А вот так сделать нельзя |
Рис. 1. Трансформация элемента
Сама матрица имеет размер 3х3 и в общем виде записывается так:
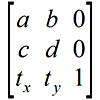
Иногда для простоты третью колонку опускают, поскольку она не оказывает влияния на конечный результат. Новые координаты каждой точки элемента после преобразования с помощью матрицы вычисляются по следующей формуле:
![]()
Роль каждого коэффициента матрицы представлена в табл. 1.
| Коэффициент | Преобразование | Описание |
|---|---|---|
| a |  |
Изменение масштаба по горизонтали. Значение больше 1 расширяет элемент, меньше 1, наоборот, сжимает. |
| b |  |
Наклон по горизонтали. Положительное значение наклоняет влево, отрицательное вправо. |
| c | Наклон по вертикали. Положительное значение наклоняет вверх, отрицательное вниз. | |
| d | Изменение масштаба по вертикали. Значение больше 1 расширяет элемент, меньше 1 — сжимает. | |
| tx | Смещение по горизонтали в пикселах. Положительное значение сдвигает элемент вправо на заданное число пикселов, отрицательное значение сдвигает влево. | |
| ty | Смещение по вертикали в пикселах. При положительном значении элемент опускается на заданное число пикселов вниз или вверх при отрицательном значении. |
Для наглядности действие каждого коэффициента вы можете проверить на данной форме (в IE не работает).
a: b:
c: d:
tx: ty:
Двумерная матрица
Преобразование с помощью двумерной матрицы происходит в плоскости экрана, при этом соблюдается условие, что линии всегда остаются параллельными, поэтому в качестве трансформации допустимы поворот, масштабирование, наклон и изменение положения, но никак не перспектива или нечто подобное. Это уже область работы трёхмерной матрицы. На рис. 1 показаны допустимые и невозможные преобразования, выполненные с помощью двумерных матриц.
 |
 |
 |
 |
| Исходный элемент | Поворот | Наклон | А вот так сделать нельзя |
Рис. 1. Трансформация элемента
Сама матрица имеет размер 3х3 и в общем виде записывается так:

Иногда для простоты третью строку опускают, поскольку она не оказывает влияния на конечный результат. Новые координаты каждой точки элемента получаются путём умножения матрицы преобразований на матрицу координат.

И вычисляются по следующей формуле:

Роль каждого коэффициента матрицы представлена в табл. 1.
| Коэффициент | Преобразование | Описание |
|---|---|---|
| a |  |
Изменение масштаба по горизонтали. Значение больше 1 расширяет элемент, меньше 1, наоборот, сжимает. |
| b | Наклон по вертикали. Положительное значение наклоняет вверх, отрицательное вниз. | |
| c | Наклон по горизонтали. Положительное значение наклоняет влево, отрицательное вправо. | |
| d | Изменение масштаба по вертикали. Значение больше 1 расширяет элемент, меньше 1 — сжимает. | |
| tx | Смещение по горизонтали в пикселях. Положительное значение сдвигает элемент вправо на заданное число пикселей, отрицательное значение сдвигает влево. | |
| ty | Смещение по вертикали в пикселях. При положительном значении элемент опускается на заданное число пикселей вниз или вверх при отрицательном значении. |
Для матрицы преобразований применяется функция matrix(), внутри скобок перечисляются коэффициенты.
transform: matrix(a, b, c, d, tx, ty)
Отражение
Для отражение элемента по горизонтали следует установить a=-1, по вертикали d=-1 или оба значения одновременно для отражения одним разом по горизонтали и вертикали.
В примере 2 показано отражение текста по вертикали.
Пример 2. Отражение
<!DOCTYPE html> <html> <head> <meta charset=»utf-8″> <title>Трансформация</title> <style> .t { transform: matrix(1, 0, 0, -1, 0, 0); } </style> </head> <body> <p class=»t»>Через миг Алиса прошла сквозь зеркало и легко спрыгнула в Зазеркалье.</p> </body> </html>
Результат данного примера показан на рис. 3.
Рис. 3. Отражение текста по вертикали
За наклон отвечают коэффициенты b и c, которые и влияют на вид элемента. Давайте установим c=1 и посмотрим, какие преобразования получатся.
x’ = 1*x + 1*y + 0
y’ = 0*x + 1*y + 0
x’ = x + y
y’ = y
Таким образом, меняется только координата x, которая увеличивается на значение y, что и приводит к наклону элемента. В примере 3 используется отрицательное значение коэффициента c для наклона вправо.
Пример 3. Наклон
<!DOCTYPE html> <html> <head> <meta charset=»utf-8″> <title>Трансформация</title> <style> .t { background: #e7685d; /* Цвет фона */ color: #fff; /* Цвет текста */ padding: 10px; /* Поля */ width: 300px; /* Ширина */ transform-origin: 0 100%; /* Точка трансформации */ transform: matrix(1, 0, -0.5, 1, 0, 0); /* Трансформация */ } </style> </head> <body> <div class=»t»> <p>То, что делает армию при встрече с противником непобедимой, это правильный бой и маневр.</p> <p>Сунь-Цзы. Искусство войны. Пер. Н. Конрад.</p> </div> </body> </html>
Результат данного примера показан на рис. 4.
Рис. 4. Наклон блока
>Перемещение
За сдвиг элемента по горизонтали отвечает коэффициент tx, а по вертикали ty. Значением выступает число пикселей.